Рабочая программа по математике 5 класс Виленкин Н. Я. ФГОСМуниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа . Агрыз Республики Татарстан«Рассмотрено»Руководитель МО: /. Агрыз РТ протокол .

Рабочая программа по математике в 5 классе ФГОС 2017-2018. Планирование. Планируемые результаты освоения учебного предмета.

Агрыз РТ на 2. 01. Она составлена на основе проекта Федерального государственного образовательного стандарта общего образования в соответствии с объ. Программа содержит следующие разделы: – пояснительная записка, в которой определяются цели и задачи обучения по данному предмету; – общая характеристика курса; – место в учебном плане; – требования к результатам обучения; – основное содержание курса с описанием соответствующих действий детей; примерное тематическое планирование с описанием ви.

Рабочая программа для учителя-предметника для 5 класса по ФГОС. Программы по Математике. Рабочая программа МАТЕМАТИКА ФГОС 5 класс. Нажмите, чтобы скачать публикацию в формате MS WORD (*.

Это предполагает особую организацию учебного процесса в форме учебной деятельности школьников. Содержание учебной деятельности должно развертываться в теоретической форме – от общего к частному, от абстрактного к конкретному. Освоение понятий должно происходить не в форме отработки словесных формулировок, а путем введения учащихся в новый круг задач и включением их в деятельность по поиску общего способа их решения. Поиск способа решения новой задачи является мотивационным ядром учебной деятельности, той ценностной установкой учеников, которая складывается в виде формального эффекта обучения как личностно- смысловое образование, основа желания и умения учиться. Необходимость поиска способа решения новой задачи не диктуется требованиями учителя, учебника или программы, она должна быть обусловлена для детей внутренней логикой содержания обучения. Когда ученики обнаруживают, что задача не может быть решена теми способами, которыми они уже владеют, они сами заявляют о необходимости поиска новых способов действия. Иными словами, уже начав действовать, уже стремясь получить результат, дети фиксируют невозможность его немедленного достижения и необходимость открытия «чего- то нового».

При этом принципиально, что поисковые действия детей (их пробы, мнения, предложения, вопросы) должны быть направлены не на внешние чувственно- представленные, непосредственно наблюдаемые свойства вещей, а на общий принцип их строения. Скачать Программу Kmsauto Бесплатно подробнее. Вскрывая этот общий принцип посредством собственных действий, осуществляемых не в словесной, а предметно- чувственной форме, ребенок тем самым обнаруживает существенное отношение, лежащее в основании нового понятия. Отношение, которое дети обнаруживают, преобразуя объект изучения, не обладает чувственной наглядностью, оно нуждается в особом – модельном способе презентации.

При этом не всякое изображение можно назвать учебной моделью, а лишь такое, которое отображает внутренние особенности объекта, не наблюдаемые непосредственно, и обеспечивает их дальнейший анализ. Учебная модель, выступая как продукт мыслительного анализа, затем сама может стать особым средством мыслительной деятельности. С одной стороны, в процессе построения модели происходит абстракция отношения от его предметных носителей. С другой стороны, уже построенная модель, в которой отношение представлено материально, позволяет преобразовывать ее, открывая новые свойства этого отношения. Преобразовывая и переконструируя учебную модель, школьники получают возможность изучать свойства отношения как такового, без «затемнения» привходящими обстоятельствами. Представленная моделью абстракция затем конкретизируется в различных частных условиях, что позволяет применять найденный общий способ к целому классу частных задач.

Для того чтобы дети смогли через собственные поисковые действия открыть новый способ действия, необходимы особые формы организации совместной учебной деятельности класса и учителя. Основой этой организации является общеклассная дискуссия, в которой каждое высказанное предложение оценивается остальными участниками обсуждения с точки зрения соответствия способа действия и достигнутого результата. Предложения учителя подлежат такому же контролю и оценке, что и предложения учеников. При этом достоинства и недостатки предлагаемых способов действия оцениваются содержательно и ученики участвуют в выработке критериев контроля и оценки наряду с учителем. Благодаря этому у школьников складывается способность к самоконтролю и самооценке как базисным компонентам умения учиться.

Осуществление школьниками учебной деятельности способствует формированию у них таких мыслительных действий, как рефлексия, анализ и планирование, являющихся основой теоретического мышления и, одновременно развитию других познавательных процессов – восприятия, воображения, памяти. Это дает основание говорить о развивающем значении специальной организации учебной деятельности школьников. В курсе математики 5 класса могут быть условно выделены четыре содержательные области: развитие понятия числа, величины и отношения между ними, элементы геометрии, элементы теории вероятностей и статистики. Первая область посвящена дальнейшему развитию понятия числа: введению новых видов чисел . Исходным отношением, порождающим все виды действительного числа, является отношение величин, получаемое в результате решения задачи измерения одной величины с помощью другой, принятой в качестве единицы измерения; меняются лишь условия этой задачи, что и определяет различия видов числа и способов его обозначения. Так различные виды дробей появляются в ситуации, когда единица не укладывается в измеряемой величине целое число раз. А введение нового свойства величины – ее направленности – позволяет из того же исходного отношения получить отрицательные числа (отрицательному числу соответствует ситуация когда измеряемая величина и единица измерения имеют противоположные направления).

Виленкин (ФГОС). Рабочая программа расчитана на использования УМК. Рабочая программа по алгебре (5 класс) на тему: Рабочая программа по математике для 5 класса ФГОС ООО на 2014-2015. Программы по Математике для 5 класса по УМК Виленкин Н.Я., Жохов В.И.и др. Рабочая программа по математике 5 класс Виленкин Н.Я. Нажмите, чтобы скачать публикацию в формате MS .

Появление каждого нового вида чисел сопровождается определением их места на координатной прямой. При этом координатная прямая выступает не как иллюстрация, а как основное средство моделирования, с помощью которого устанавливаются свойства чисел и способы действий с ними, которые лишь затем «отрываются» от координатной прямой и приобретают алгоритмические формы. Тем самым к концу 5 класса у учащихся формируется представление о системе действительных чисел. К этой же содержательной области отнесен ряд вопросов, связанных с формальной стороной использования чисел: вычисление значений числовых и буквенных выражений, решение линейных уравнений и простейших неравенств, изображение их решений на координатной прямой, описание числовых промежутков. Вводится координатная плоскость, рассматривается построение и описание простейших линий и областей на координатной плоскости.

Рабочая программа МАТЕМАТИКА ФГОС 5 класс. ПОЯСНИТЕЛЬНАЯ ЗАПИСКАРабочая программа по математике составлена на основе следующих нормативных документов и методических рекомендаций: учебник «Математика», 5 класс С. Н. Никольский и др., М. Просвещение, 2. 01. М. Просвещение, 2. Программой предусмотрено проведение 9 контрольных работ.

Рабочая программа ориентирована на использование учебно- методического комплекса: Математика 5 класс: учебник для общеобразовательных учреждений. Никольский, М. Решетников, А. Шевкин – Изд. Потапов, А В.

Шевкин – М.: Просвещение, 2. Математика 5 класс: рабочая тетрадь по математике: пособие для учащихся общеобразовательных учреждений/ М. Шевкин – М.: Просвещение, 2. Математика 5 класс: тематические тесты/ П.

Зарапина - М.: Просвещение, 2. Математика 5 класс: книга для учителя/ М. Шевкин – М.: Просвещение, 2. Задачи на смекалку 5 класс: И. Шарыгин пособие для учащихся общеобразовательных учреждений/- М.: Просвещение, 2. ОБЩАЯ ХАРАКТЕРИСТИКА УЧЕБНОГО ПРЕДМЕТА «МАТЕМАТИКА»Математическое образование играет важную роль в практической жизни общества, которая связана с формированием способностей к умственному эксперименту. Практическая полезность предмета обусловлена тем, что происходит формирование общих способов интеллектуальной деятельности, значимой для различных сфер человеческой деятельности.

Обучение математике дает возможность формировать у обучающихся качества мышления необходимые для адаптации в современном информационном обществе. Новизна данной программы определяется тем, что в основе построения данного курса лежит идея гуманизации обучения, соответствующая современным представлениям о целях школьного образования и уделяющая особое внимание личности ученика, его интересам и способностям. Предлагаемый курс позволяет обеспечить формирование как предметных умений, так и универсальных учебных действий школьников, а также способствует достижению определённых во ФГОС личностных результатов, которые в дальнейшем позволят обучающимся применять полученные знания и умения для решения различных жизненных задач. При организации процесса обучения в рамках данной программы предполагается применение следующих педагогических технологий обучения: личностно- ориентированная (педагогика сотрудничества), позволяющую увидеть уровень обученности каждого ученика и своевременно скорректировать её; технология уровневой дифференциации, позволяющая ребенку выбирать уровень сложности; информационно- коммуникационная технология, обеспечивающая формирование учебно- познавательной и информационной деятельности учащихся.

ОПИСАНИЕ МЕСТА УЧЕБНОГО ПРЕДМЕТА В УЧЕБНОМ ПЛАНЕ Программа рассчитана на 1. Римская нумерация. Ряд натуральных чисел.

Десятичная запись, сравнение, сложение и вычитание натуральных чисел. Законы сложения. Умножение, законы умножения. Степень с натуральным показателем.

Деление нацело, деление с остатком. Числовые выражения.

Решение текстовых задач. Измерение величин (3. Прямая, луч, отрезок. Измерение отрезков и единицы длины. Представление натуральных чисел на координатном луче. Окружности и круг, сфера и шар. Углы, измерение углов.

Треугольник, прямоугольник, квадрат, прямоугольный параллелепипед. Площадь прямоугольника, объем прямоугольного параллелепипеда. Единицы массы, времени.

Решение текстовых задач. Делимость натуральных чисел (1. Свойства и признаки делимости. Простые и составные числа. Делители натурального числа. Наибольший общий делитель, наименьшее общее кратное. Обыкновенные дроби (6.

Понятие дроби, равенство дробей (основное свойство дроби). Приведение дробей к общему знаменателю. Сравнение, сложение и вычитание любых дробей. Законы сложения. Умножение дробей, законы умножения. Деление дробей. Смешанные дроби и действия с ними. Представления дробей на координатном луче. Решение текстовых задач.

Итоговое повторение курса математики (1. Ряд натуральных чисел. Десятичная запись, сравнение, сложение и вычитание натуральных чисел.

Законы сложения. Умножение, законы умножения. Степень с натуральным показателем. Деление нацело, деление с остатком. Числовые выражения. Решение текстовых задач. Обыкновенные дроби.

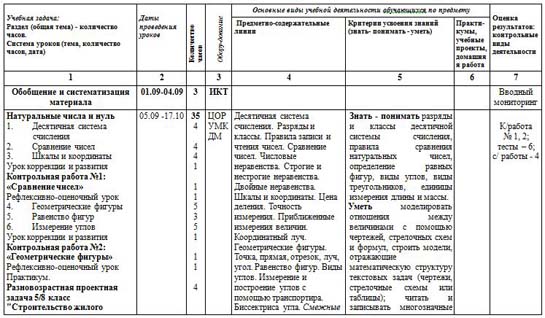
Решение задач на движение по реке и совместную работу. Вычисление площади прямоугольник и объема прямоугольного параллелепипеда. ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ ПО ПРЕДМЕТУ «МАТЕМАТИКА» .

Десятичная запись чисел. Многозначные числа.

Состав числа. Таблица классов и разрядов. Определяют разряд числа, знакомятся с понятиями многозначные числа, состав числа, записывают числа в виде разрядных слагаемых, решают логические задачи на запись натуральных чисел, самостоятельно контролируют своё время и управляют им, аргументируют свою точку зрения. Таблица классов и разрядов. Целые положительные числа.

Ряд неотрицательных целых чисел. Знакомятся с понятиями больше, меньше, неравенство, равенство; сравнивают натуральные числа с помощью натурального рада; записывают результаты сравнения с помощью знаков сравнения; записывают неравенства, используя буквенную запись; выделяют характерные причинно- следственные связи, строят речевое высказывание в устной форме, аргументируют свою точку зрения, реализуют основы исследовательской деятельности, оказывают в сотрудничестве необходимую взаимопомощь    Решение задач по теме «Сравнение натуральных чисел»Сравнение натуральных чисел. Компоненты суммы чисел. Использование натурального ряда для нахождения суммы натуральных чисел Формулируют и записывают законы сложения, выполняют сложение с помощью натурального ряда, применяют законы сложения рационализации вычислений к решению задач, аргументируют свою точку зрения, самостоятельно контролируют своё время и управляют им    Законы сложения. Законы сложения (переместительный, сочетательный) Буквенная запись законов. Использование натурального ряда для нахождения разности натуральных чисел.

Используют названия компонентов действия при вычитании, выполняют вычитание с помощью натурального ряда, применяют вычитание к решению задач, проводят сравнение, владеют устной и письменной речью, осуществляют взаимный контроль    Решение задач по теме «Вычитание»Решение текстовых задач на сложение и вычитание. Компоненты произведения чисел. Законы умножения (переместительный, сочетательный). Буквенная запись законов.